Jacobi equation
Also known as geodesic deviation equation, it relates geodesics and Gaussian curvature.
This equation describes how the separation between geodesics (as measured by a Jacobi field) evolves as we move along the geodesics.
The equation is
$$ \frac{D^2}{dt^2} J + R(J, U)U = 0, $$with the notation given here.
In surfaces
In a 2-dimensional Riemannian manifold, the Riemann curvature tensor simplifies significantly. In particular, it can be expressed entirely in terms of the Gaussian curvature $K$. The Riemann curvature tensor in 2 dimensions is given by:
$$ R(X, Y)Z = K(g(Y, Z)X - g(X, Z)Y), $$where $X, Y, Z$ are vector fields on the manifold, $g$ is the metric tensor, and $K$ is the Gaussian curvature.
So substituting this in the Jacobi equation we obtain
$$ \frac{D^2}{dt^2} J + K(g(U, U)J - g(J, U)U) = 0. $$If the geodesic has a unitary tangent vector the equation simplifies to:
$$ \frac{D^2}{dt^2} J + K(J-g(J, U)U ) = 0. $$Intuitive approach of Needham
Case $n=2$
In a surface
$$ \ddot{\xi}=-\mathcal{K}\xi $$being $\xi(t)$ the "separation" of two geodesics (@needham2021visual page 269; and proof in 274)
Proof
It uses geodesic polar coordinates. Also uses Gauss lemma.
By the way, it let us to show Minding's theorem.
$\blacksquare$
Formal statement is based on the notion of Jacobi field.
Case $n>2$
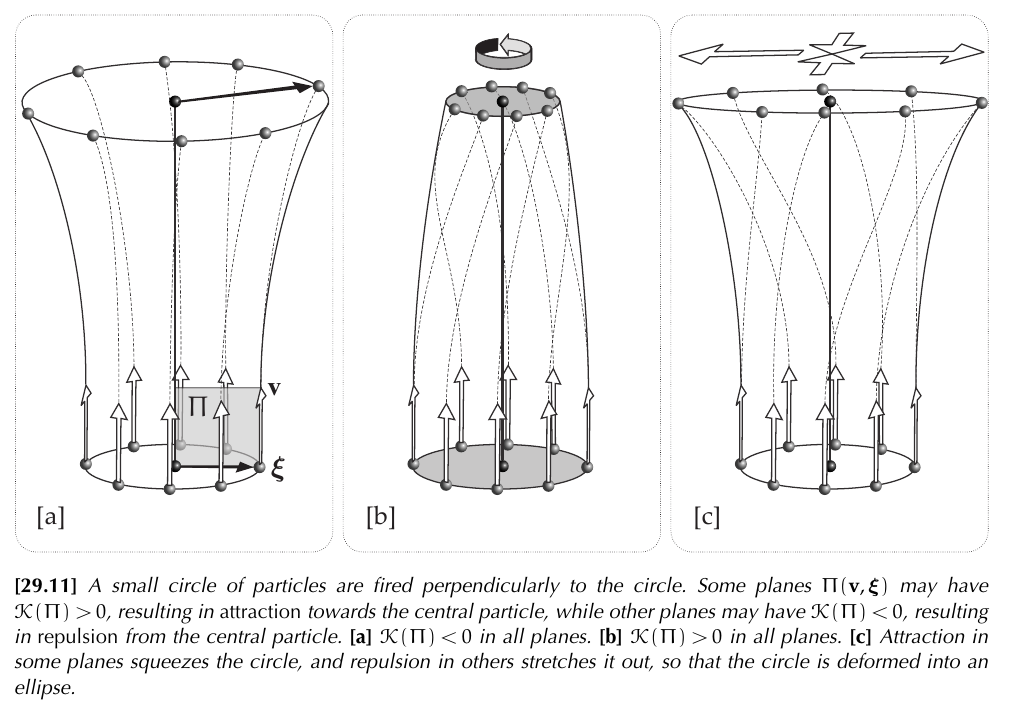
According to @needham2021visual there are two versions:
- Sectional Jacobi equation
where $\Pi$ is a plane containing the tangent vector $v$ to the geodesic, $\mathcal{P}$ is the projection over this plane and $\mathcal{K}(\Pi)$ is the sectional curvature.
- General Jacobi equation or Equation of Geodesic Deviation
When $\mathcal{R}(\boldsymbol{\xi}, \mathbf{v}) \mathbf{v}$ is not contained in $\Pi$ it happens the rotation of picture b) above.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: